TLDR: We raced in an urban orienteering challenge last Sunday and won a the male category champion with finish time 3:07. The female category champion led us by 7min, which is a huge margin to ensure them to be overall champion. I tried to construct an optimal solution using Travelling Salesperson Problem (TSP) and found out we could have saved about 2KM in leg distances, which roughly maps to 12 minutes.

About the race

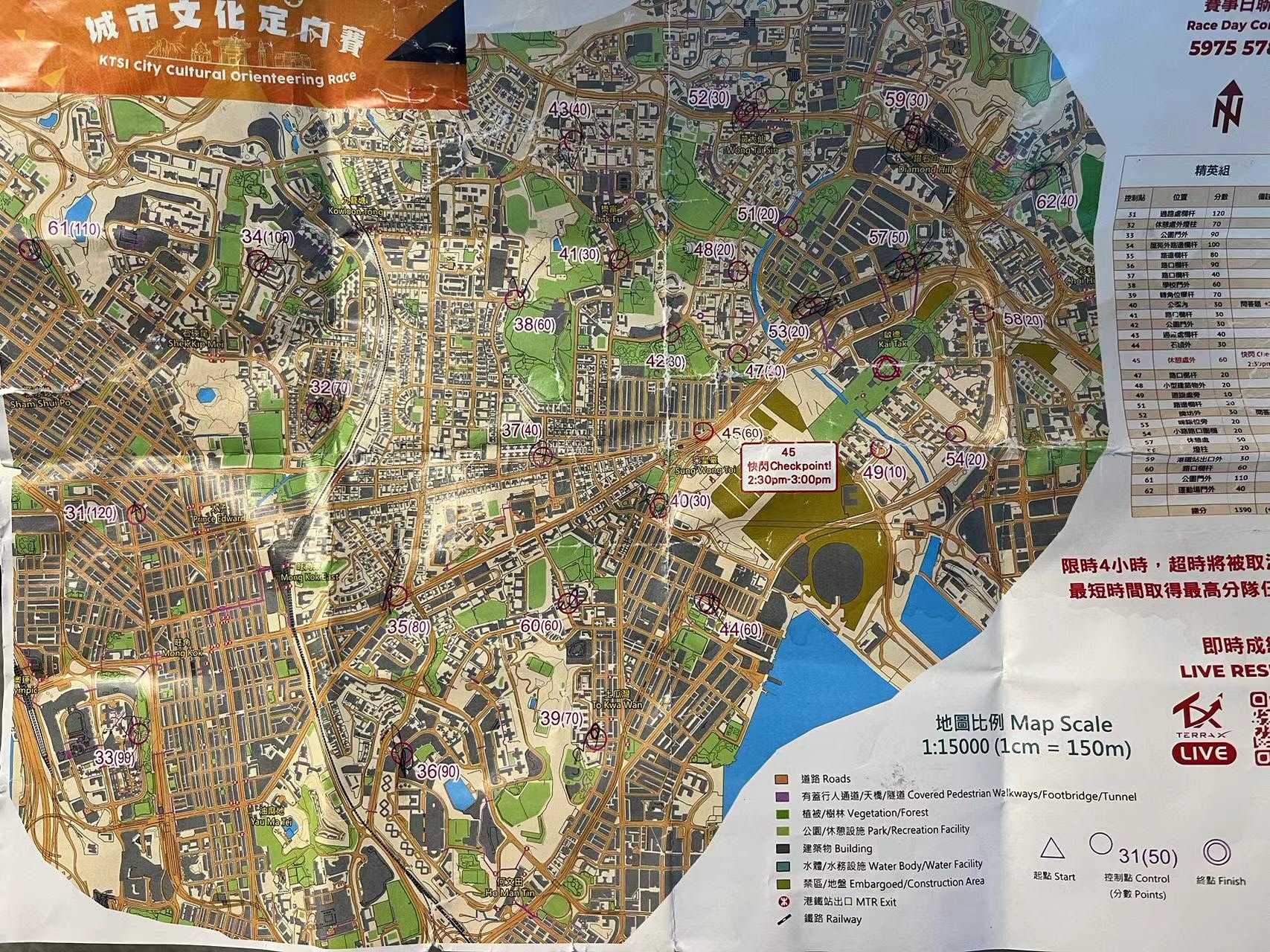
Sketch of the urban orienteering challenge:

• There are 28 check points.
• Teams must run together and visit each check point together.
• Teams start from START and return to the location within cutoff time (4-hour in our case).
• Each check point has different award points.
• Award points can vary based on quizzes/ team challenges at each checkpoint.
• Final ranking is based on: max total award points, minimum finish time.
• One check point is a flash check point which is only open during 2:30pm-3:00pm.
• Teams can use public transport like bus/ MTR, but not private transport (private cars/ taxi).
• Each team is given a paper map upon start, which is a "cartogram", i.e. distorted version of real map. The length / distance may look different from reality but the relative positioning is kept intact.
• It was not specified if cell phone is allowed.
• The race is self supported. There is no water station.

Get pairwise distances

We use the Google Maps Platform Distance Matrix API.

First follow the official docs to get API key and store in the variable key.

One constraint of the API is that max origins/ destinations per query is limited to 25. There are 29 points in our problem, so we need to issue several batches of requests and construct the sub matrix in a double loop.

import requests

def get_distances(origins, destinations):
  origins_str = '|'.join([f'{p[1]},{p[0]}' for p in origins])
  destinations_str = '|'.join([f'{p[1]},{p[0]}' for p in destinations])
  url_prefix = f'https://maps.googleapis.com/maps/api/distancematrix/json'
  params = {
    'destinations': destinations_str,
    'origins': origins_str,
    'units': 'KM',
    'key': key,
    'mode': 'walking',
  }
  r = requests.get(url_prefix, params=params)
  matrix = []
  for row in r.json()['rows']:
    row_values = []
    # print(row['elements'])
    for e in row['elements']:
      row_values.append(e['distance']['value'])
    matrix.append(row_values)
  return matrix

def get_pairwise_distances(points, chunk=10):
  re = []
  for _ in range(len(points)):
    re.append([None] * len(points))
  for i in range(0, len(points), chunk):
    for j in range(0, len(points), chunk):
      print('i', i, min(i + chunk, len(points)))
      print('j', j, min(j + chunk, len(points)))
      origins = points[i: min(i + chunk, len(points))]
      destinations = points[j: min(j + chunk, len(points))]
      m = get_distances(origins, destinations)
      # print(m)
      for p in range(len(m)):
        for q in range(len(m[p])):
          re[i + p][j + q] = m[p][q]
  return re

I use Google Custom Map to mark those points on my paper map and export a CSV containing the data. Then I upload the CSV to Google Drive and open with Google Sheets. From this point onward, we can use Sheets API to read the data directly.

from google.colab import auth
from google.auth import default
import gspread
import gspread_dataframe

auth.authenticate_user()
gc = gspread.authorize(default()[0])

s = gc.open_by_key('HERE IS THE DOCUMENT KEY OF SHEETS')
df = gspread_dataframe.get_as_dataframe(s.sheet1)

# Read check point data
check_points = df[~df['WKT'].isna()]['WKT', 'name'](https://hash.hupili.net/wkt-name/)
point_tuples = check_points['WKT'].apply(lambda x: x.split('(')[1].split(')')[0]).apply(lambda t: t.split()).values
names = check_points.name.values

Solve with pyconcorde

This section follows exactly the blog post of Mike Jones . Please see the original blog for explanations. I copied the codes below for completeness of current writing.

Install the libs:

git clone https://github.com/jvkersch/pyconcorde # clone git repo
cd pyconcorde                                    # change directory
pip install -e .                                 # install pyconcorde

pip install folium

Massage the pair wise distances into the right shape for concorde solver.

def symmetricize(m, high_int=None):

    # if high_int not provided, make it equal to 10 times the max value:
    if high_int is None:
        high_int = round(100*m.max())

    m_bar = m.copy()
    np.fill_diagonal(m_bar, 0)
    u = np.matrix(np.ones(m.shape) * high_int)
    np.fill_diagonal(u, 0)
    m_symm_top = np.concatenate((u, np.transpose(m_bar)), axis=1)
    m_symm_bottom = np.concatenate((m_bar, u), axis=1)
    m_symm = np.concatenate((m_symm_top, m_symm_bottom), axis=0)

    return m_symm.astype(int) # Concorde requires integer weights

from concorde.problem import Problem
from concorde.concorde import Concorde

def solve_concorde(matrix):
    problem = Problem.from_matrix(matrix)
    solver = Concorde()
    solution = solver.solve(problem)
    print(f'Optimal tour: {solution.tour}')
    return solution

m_bar = symmetricize(np.matrix(m))
solution = solve_concorde(m_bar)

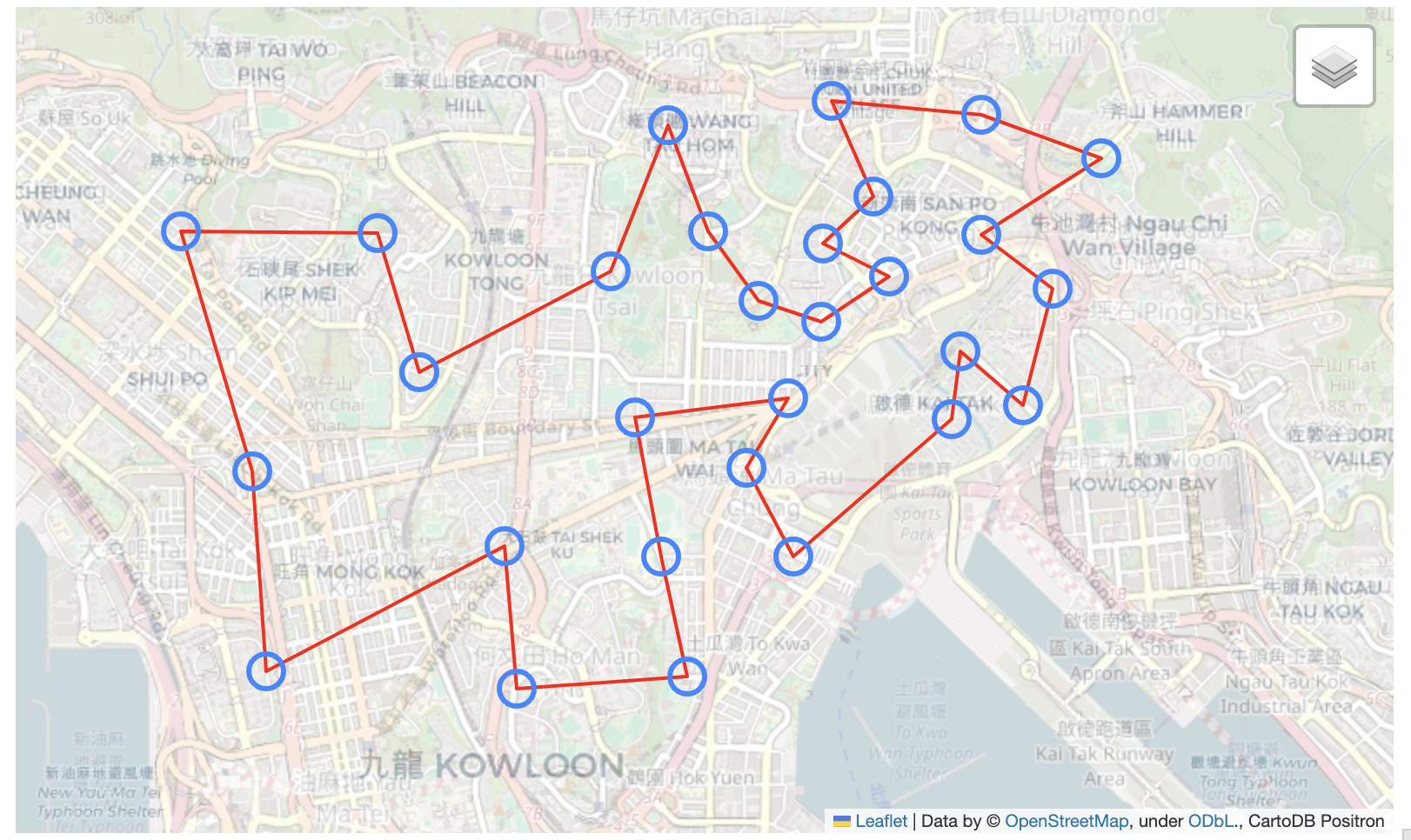
In our problem, we get the solution.optimal_value=28336, and solution.tour encodes the sequence to visit each check point.

The solution can be visualized with folium as follows:

# pick alternate elements: these correspond to the originals
tour = solution.tour[::2]

# order the original coordinates and names
coords_ordered = [point_tuples[i] for i in tour]
names_ordered = [names[i] for i in tour]

# add back in the first for a complete loop
coords_ordered_return = coords_ordered + [coords_ordered[0]]

coords_ordered = np.array(coords_ordered).astype(float)
coords_ordered_return = np.array(coords_ordered_return).astype(float)

import folium
def generate_map(coordinates, names, directions=None):

    # folium needs lat, long
    coordinates = [(y, x) for (x, y) in coordinates]
    route_points = coordinates #[(y, x) for (x, y) in directions]
    lat_centre = np.mean([x for (x, y) in coordinates])
    lon_centre = np.mean([y for (x, y) in coordinates])
    centre = lat_centre, lon_centre

    m = folium.Map(location=centre, zoom_start=1, zoom_control=False)

    # plot the route line
    folium.PolyLine(route_points, color='red', weight=2).add_to(m)

    # plot each point with a hover tooltip  
    for i, (point, name) in enumerate(zip(coordinates, names)):
        folium.CircleMarker(location=point,
                      tooltip=f'{i}: {name}',
                      radius=10).add_to(m)

    custom_tile_layer = folium.TileLayer(
        tiles='http://{s}.basemaps.cartocdn.com/light_all/{z}/{x}/{y}.png',
        attr='CartoDB Positron',
        name='Positron',
        overlay=True,
        control=True,
        opacity=0.7  # Adjust opacity to control the level of greying out
    )

    custom_tile_layer.add_to(m)
    folium.LayerControl().add_to(m)

    sw = (np.min([x for (x, y) in coordinates]), np.min([y for (x, y) in coordinates]))
    ne = (np.max([x for (x, y) in coordinates]), np.max([y for (x, y) in coordinates]))
    m.fit_bounds([sw, ne])

    return m

mymap = generate_map(coords_ordered_return, names_ordered)
mymap

The colab / jupyter notebook can show object mymap as interactive map directly.

Reflections and future work

• The optimal solution given by concorde is 28.3KM whereas we ran 29.87 KM on the race day. There were a few out-and-back checkings from main road where I stayed static while waiting for my teammate to tap the reader. In that case, he ran more than 30K. We roughly ran 2KM more than the optimal solution, which based on our race day average pace means +12.5 min.
• The rules allow to use public transportation like bus or MTR. When the transport arrives right in time and along our moving direction, we can use them to save time, and more importantly to save energy / get recovered. We were not familiar with this urban area and did not risk to find the alternative solutions.
• There is a flash check point, where one can only check during 2:30pm-3:00pm. We did not put this constraint into our TSP solver.
• We did not carry water to exchange for speed. However, the race span of 3-4 hours is very long. We ended up buying water three times, even under this cold weather. For the first time, I needed to catch with my teammate after buying water and lost sight of him a few hundred meters into the road. It took some time to catchup, let alone the mental exhuastion locating him during the race setting. For the third time, I queued in 711 for about 1 minute, and it turned out one person in the front was dealing a very complex issue. I gave up buying the bottle and sped up to catch up my teammate in case I lost track again. If I were to do the race again, I'd rather carry 2L water in backpack, so that we can focus on main track.
• One variant of the problem is to set cutoff time smaller, e.g. 2 hours. In that case, no teams can collect all the check points. The problem is not TSP anymore. The formulation requires to solve the optimal visit sequence to collect maxium award points -- not that award points vary and is not absolutely proportional to the number check points collected.